The Fractal Phenomenon

How long is the coast of Britain? Would you be surprised if I told you that it’s infinitely long? Infinite coastlines are just one of many byproducts of the strange mathematics of fractal geometry.

Why is geometry often described as “cold” and “dry?” One reason lies in its inability to describe the shape of a cloud, a mountain, a coastline, or a tree. Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.

— Benoit Mandelbrot

For centuries mathematicians and philosophers were dogged by a nagging problem. Classic Euclidean geometry, with its regular lines and planes and solids, was elegant and useful, but fell down when it came to describing the natural world. It was ill-equipped to describe the seemingly endless spatial complexity of a leaf — or, for that matter, a section of coastline. Indeed, it’s largely the very presence or absence of such chaotic complexity that we subconsciously use when we decide whether something is natural or human-made. The world humanity has built is created in the image of our geometry, while the universe that birthed us, even the very forms that enclose us, is defined by its refusal to conform to our ideals of coordinates and shapes and angles. To believe that the universe is somehow corrupted or deformed because of this refusal would be the height of hubris. “These are not natural irregularities, but with respect to our fancy only; nor are they incommodious to the true uses of life and the design of man’s being on earth,” wrote Richard Bentley in the time of Swift and Pope. Yet how to reconcile the riot of natural beauty with the cooler constructions of Euclid? Until very recently we literally lacked a mathematical language to describe the world around us.

In 1975 the Polish/French mathematician Benoit Mandelbrot provided such a language when he published his theory of fractal geometry. Mandelbrot discovered that certain solution sets to certain equations generate what he called “fractals” — patterns that are infinitely detailed. Such sets were much better suited to describe natural forms than anything heretofore present in the geometric arsenal.

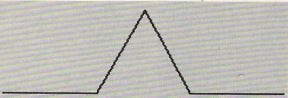
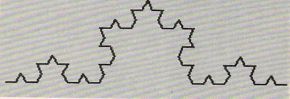
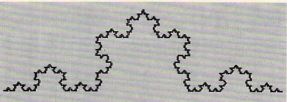
It’s this seeming paradox of infinite detail that’s the thorniest conceptual part of natural forms and fractal geometry alike. To begin to get a handle on it, consider the “snowflake” curve, an idea first proposed by Helge von Koch in 1904. Imagine that you start with a line forming a simple geometric motif.

Now you replace every straight-line segment with another copy of the original motif.

You do it again…

And you keep on doing it over and over and over, to infinity.

As you look at a coastline or a leaf at ever greater levels of magnification, there are always more details, more curves and changes to discover. This continues forever — or at least until you hit the level of individual particles of matter, the sort of resolution limit of the universe itself. Thus that aforementioned infinite — or at any rate unmeasurable — coastline. “Coastline length turns out to be an elusive notion that slips between the fingers of one who tries to grasp it,” wrote Benoit Mandelbrot. “All measurement methods ultimately lead to the conclusion that the coastline’s length is very large and so ill-determined that it is best considered infinite.”  What to make of such a logical monstrosity?

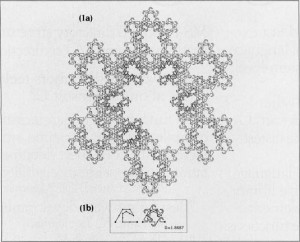
Mandelbrot found a way out in some theories of dimensionality espoused by the controversial German mathematician Felix Hausdorff more than half a century before. The easiest way to describe conventional notions of dimensionality mathematically is to say that an object’s number of dimensions equates to the number of numbers needed to describe a single point on it. Thus a line (X) is one-dimensional; a plane (X and Y) two-dimensional; a solid (X, Y, and Z) three-dimensional. Hausdorff, however, floated the counter-intuitive notion that dimensions could be fractions as well as whole numbers. Consider a line. As it gets more wiggly, ever more complex in its gyrations, its dimensionality increases, until it becomes infinitely wiggly, and completely fills — or, perhaps better said, becomes — a plane. The pattern labelled 1a below, for example, is made up of infinite repetitions (within the bounds of the resolution of the picture) of the hook-like line segment labelled 1b. According to Hausdorff’s formulation, it has a dimensionality of 1.8687.

This idea of fractional dimensionality is a strange one, but seeing complex lines in terms of dimension rather than distance does allow us to dodge the paradox of infinite coastlines, restoring a mathematical order in which the coast of Britain is again longer than that of, say, the island where I live these days, Funen.

The most interesting fractal equations are not those like the ones shown above that simply repeat a pattern, but rather those that echo themselves but never exactly repeat, to infinity. The classic example is one of the first discovered by Mandelbrot himself, the appropriately named Mandelbrot set, consisting of all solutions to (z(n) ← z(n – 1)² + c) which converge toward zero rather than expanding toward infinity. (Whilst trying to avoid getting too far down into the weeds here: this notation represents a potentially infinite series of iterations, in which n represents the current iteration. The result of the previous iteration — represented as z(n – 1) — is used as input for the next. The variable c is assumed to be a complex number, meaning it can be plotted onto the X and Y axes of a Cartesian coordinate system.)

The Mandelbrot set produces the most famous and immediately recognizable visual pattern in the field of fractals.

At this point I’d like to give you a chance to explore the Mandelbrot set for yourself, via the little program embedded below. You can pan around by holding down the left mouse button and dragging in the desired direction; drill down deeper into the image by holding down the right button and dragging to select the region you’d like to magnify; and undo each step you’ve previously made by clicking the middle button. Notice how this infinite space is made up of similar patterns that are nevertheless never quite exactly the same.

Now for the caveats: as you zoom in to ever-greater levels of magnification, the picture begins to break down and lose detail. This is not a reflection of the pure mathematics of fractal geometry, but rather a byproduct of the computing reality of limited number precision and limited processing power, especially given that this is implemented in the relatively slow language of JavaScript. Any computerized exploration of fractals is inevitably bounded by such considerations, as well as by the resolution of the individual pixels that form the patterns. Eventually my program will not let you zoom in further at all, a concession to these realities; when you reach the point that your zooms don’t take anymore, you’ll have to zoom out by clicking the middle button to continue your explorations. Due to its processing demands, not to mention the lack of handy mouse buttons, I don’t recommend that you try to play with this program on your phones or tablets. (If these limitations smart, you might want to consider how far we’ve come; a typical 68000-based computer of the 1980s would have required hours to generate each new image.)

Update: as of January 10, 2023, the website which originally hosted this toy is no more. What you see below is an archived version. You can still play with it, but it may be a bit slow to load, and the source code is no longer available.

As useful and oddly beautiful as fractal lines like the ones produced by the Mandelbrot set can be, they’re only the beginning. Fractal planes are also possible, existing in some fractional limbo between two and three dimensions. Just as a plane is in this formulation an infinitely complicated line, a solid is an infinitely “wrinkled” plane. And just as fractal lines are perfect for representing coastlines and leaves, fractal planes can easily become mountains. The striking pictures shown below were computer-generated by Richard F. Voss in 1983 using only fractal equations.

It’s also possible — mathematically, that is — to go further, to produce fractals that strain toward a fourth (or higher) dimension. However, representing them becomes a problem given our three-dimensional world. We can only show a three-dimensional slice of these fractals. Doing so produces some strange shapes indeed, like the “dragons” of Alan Norton.

Benoit Mandelbrot published his magnum opus, The Fractal Geometry of Nature, in 1982; it still remains the definitive book on the subject. It’s a strange sort of mathematics text, in which Mandelbrot devotes at least as much space to philosophical digressions into the implications of his discoveries as he does to proofs and equations, and that much space again to lots of beautiful color slides of the fractals themselves. With the book’s publication, the theory of fractals became an example of a rare phenomenon indeed: a development in abstract higher mathematics that was taken up and trumpeted widely and excitedly by not just the likes of Scientific American (which devoted many, many articles to the subject) but also mainstream magazines, newspapers, even television broadcasts. As is all too typical of any new media plaything, fractals were hyped as useful for everything short of curing cancer — and I suspect that some wouldn’t put that past them either. Not only could physicists use them to understand the motions of molecules and biologists to understand the growth of plants, but some researchers claimed that fractal music was a possibility, while others claimed that they could help you get rich by revealing the “hidden patterns” that govern the stock market. In a 1984 article for Byte magazine, Peter R. Sørensen waxed effusive: “their uses range from physics, biology, and sociology, to art and even motion-picture scene simulation.” While I’m hardly qualified to speak to their uses in the former three scientific disciplines, I do feel fairly confident in claiming that they have had the greatest impact on those latter two, mushier categories, especially if we preface “art” with the word “computer” and allow computer games to slip in under that label.

Tellingly, Mandelbrot was employed at IBM’s Thomas J. Watson Research Center at the time he wrote The Fractal Geometry of Nature; all of the images found within it were generated by the computers there. Many fractal equations, including some of the most beautiful, aren’t complex at all in themselves, but the need to iterate through them so many times to produce their solution sets means that the science of fractals could exist only as a theory without the aid of computers. The first primitive computerized fractal visualizations had been produced by Robert W. Brooks and Peter Matelski in 1978, just three years after Mandelbrot first codified his theories. Virtually from that time forward fractals were inseparable from the computers needed to properly generate and study them.

Many people got their first glimpse of fractals before the hype started in earnest, in a remarkable sequence of computer-generated special effects included in 1982’s Star Trek II: The Wrath of Khan.

The creators of the sequence were the Lucasfilm Graphics Group, a collection of software and hardware engineers whom George Lucas had started putting together in 1979. These folks, whose numbers included such soon-to-be computer-graphics legends as Alvy Ray Smith, designed and built all of the hardware and software used to create sequences like this one. In 1986, the Graphics Group would be spun off to become an independent company whose name you might know: Pixar.

When Lucasfilm elected to start a computer-games division shortly after the sequence shown above was created, it was natural for it to draw inspiration, technologies, and even personnel from the Graphics Group. One of Lucasfilm’s first two games, Rescue on Fractalus!, proudly bears its graphical underpinnings and its status as the first game to make significant use of fractals right there in its title. (By way of continuing the theme, the alien enemies you fight are called the “Jaggies,” a reference to the ugly pixelized artifacts that are one of a computer artist’s worst enemies.) The game sparked great interest from its first press preview in May of 1984, thanks to its endlessly varied mountainous terrain, generated on the fly using fractal algorithms.

In the wake of Rescue on Fractalus! fractals were suddenly everywhere in the computing press; I’m not sure there was a single magazine that didn’t publish at least one big feature article on the subject over the next few years. The appeal of fractals to programmers was obvious, and had little to do with Mandelbrot’s esoteric philosophies about geometry and nature. Irregular, natural-looking landscapes had previously been dauntingly hard to craft for games — hard not only because they were a pain to draw but also and predominately because they were so un-amenable to compression algorithms and, indeed, to virtually all of the many innovative techniques programmers had discovered to store graphics data using minimal memory. Thus the distinctly regular, blocky graphics that were the norm, and the shock that was Rescue on Fractalus! Much like the Fibonacci-derived galaxies of Elite, fractals let programmers create whole landscapes generatively, from only an equation and a few seed numbers. They had their limitations, not least the amount of processing power that had to be allocated to generating them — Rescue on Fractalus! runs at all of 5 or 6 frames per second — but for many applications they seemed like magic. It was not a coincidence that after 1984 virtual landscapes started to become markedly richer and more natural.

But fractals did more than just make games prettier; they opened up whole new realms of possibility for them. The bit of video below, from a remarkable game that will be the topic of another article I’ll be publishing soon, may not look like much in contrast to some of what you’ve already seen today. Yet consider that, thanks to the magic of fractals, the planet being landed on is one of thousands to be topographically mapped in its entirety, and that you can land on it absolutely anywhere you like, zooming in from space to touch down where you will just as you can zoom and pan and explore the Mandelbrot set via the toy embedded into this article. Each of these unique worlds is generated using just a few numbers, a bare handful of bytes of precious memory.

Fractals aren’t quite the media darlings they once were; many other shiny objects have come and gone since the 1980s. And while they remain a valuable tool in many branches of science, they’re no longer viewed there either as the revolution they once were. You certainly don’t hear much anymore about fractal music or using fractals to play the stock market. Likewise, they’re now just another item in a game programmer’s bag of tricks. Still, they retain a fascination and beauty all their own. In that spirit, have fun in any further explorations you undertake, and if you discover any interesting patterns using my little toy above, or if you create any enhancements on the Studio Sketchpad site that hosts it, by all means let me know.

(As noted in the article proper, old computer magazines are an embarrassment of riches when it comes to information on fractals. Particularly good articles are found in the Byte of March 1984, September 1984, and June 1986; the 80 Microcomputing of December 1984; the Ahoy! of April 1987; the Amazing of March 1989, July 1989, October 1989, January 1990, June 1990, and April 1991; the Compute! of January 1983; and the A.N.A.L.O.G. of January 1986.

And since we’re in a multimedia sort of mood today, check out this song about the Mandelbrot set, sent to me by reader Rick Reynolds.)